Writing a simple Sudoku solver in Python
What is a Sudoku puzzle? #
I assume you are familiar with Sudoku puzzles , but let’s look at an example.
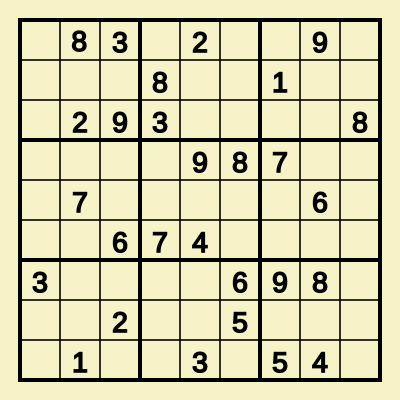
Here is a ‘diabolical’ Sudoku puzzle from the Sudoku exchange puzzle bank that we are going to solve.
83| 2 | 9
|8 |1
29|3 | 8
---+---+---
| 98|7
7 | | 6
6|74 |
---+---+---
3 | 6|98
2| 5|
1 | 3 |54
As you probably know, the goal is to fill the blanks 9x9 grid, such that digits 1 through 9 appear once in every row, column and 3x3 box.
In the puzzle bank, puzzles are given as an 81-character string, listing the digits in reading order, with 0 used to indicate blank cells. Here is the same puzzle in this format, which we will also use in our program:
083020090000800100029300008000098700070000060006740000300006980002005000010030540
Preparations #
Before we start, let’s take a look at the elements of the puzzle.
A standard 9x9 Sudoku consists of a square grid with 81 cells.
The Sudoku puzzle has 9 rows, which we will number 0 through 8 from top to bottom. Usually the top row is called row 1, but for programming it is often convenient to start with 0, since list indices start at 0.
Similarly, we number the 9 columns 0 through 8 from left to right.
The nine 3x3 boxes will also be numbered 0 through 8, starting at the top left box in reading order:
0 1 2
3 4 5
6 7 8
Now let’s think about how to solve the puzzle automatically. For human solvers there are various tactics for solving that we could try to implement. For this tutorial however, we will be using using a backtracking algorithm. This is a brute force algorithm that isn’t too smart, but just tries all possibilities until a solution is found.
Backtracking #
Backtracking works by trying all possible digits for an empty cell, and then recursively trying to solve the remaining puzzle. Recursively means that we use the same backtracking algorithm to solve the remaining puzzle.
In order to understand this approach, let’s start with a simpler problem: opening a padlock with a 3-digit code.

If we forgot the code, we can go through all the possible codes 000-999. This is a brute force method, since it doesn’t involve clever tricks but just tries everything. However, in some cases we can do less work.
Going through all possible codes in order, means we first guess the first digit. To keep track of what we’ve tried, we guess the possible digits in order, so first 0, then 1, and so on until 9. So to begin, we guess the first number is 0.
Now we try to find the complete code by guessing the remaining two numbers. The first clever trick is that this is just a simpler lock with only two digits, so we can use the same procedure: we guess the first of these two numbers (i.e. the second of the three digits) to be 0.
Now we are left with the third digit, so basically a 1-digit lock. Again, we start by guessing 0. If the lock doesn’t open, we try the next number (1), and continue until we’ve tried all digit.
If the lock didn’t open, we couldn’t solve the 1-digit lock, so we must have done something wrong earlier. We take one step back (hence backtracking) to the second number, for which we guessed 0. We change it to 1 for our next guess, and again try to solve the remaining 1-digit code by trying all possibilities for the third digit.
We repeat the process until the lock opens, or until we’ve ran out of possibilities at 099. If the lock is still closed, we have to backtrack to the first digit: try 1 instead of 0 and repeat the process. This will try all combinations from 100 to 199.
So far this seems like a complicated way of describing how to try all 3-digit numbers, but we’ve made a big step to an algorithm. Whatever the number of digits on the lock, we only have to try all possibilities for the first digit and then use our solving method on the remaining digits. We now have a general, recursive (calling itself) approach:
# lock with a 3-digit code
combinations = ['0', '0', '0']
# try all different digits for given position
def try_digits(position):
# if we ran out of positions to try, we can return
if position == len(combinations):
# we now have a guess for all positions, so
# we can try to open the lock.
# instead, we just print the combination for now.
print(combinations)
return
for digit in '0123456789':
# fill in our guess for the current position
combinations[position] = digit
# recursively solve the remaining digits
try_digits(position + 1)
# try all combinations, starting at position 0
try_digits(0)
This program tries all codes from 000-999. We could have just looped trough all integers in this range, but the recursive approach is nice because it can focus on only 1 digit and leave the rest of the digits to the recursive call.
Note that this is a pretty generic program that isn’t specific for 3-digit codes. If you set combinations to a longer list of zeroes it will work for other lengths without modifications.
Until now we just tried all numbers, but let’s say that we remember that the first digit must be even. Now, if starting with 0 does not give a solution, we don’t have to try all numbers starting with 1. We already know that the code is wrong, so there’s no need to try all 100 possibilities (00-99) for the remaining two digits. By stopping as soon as we know we are on the wrong track, we can save a lot of work.
Think of the number of possibilities for a sudoku grid. If there are 20 digits given, we still need to guess the remaining 61 digits. If we put those together, we would get all 61-digit numbers without 0. Those are way too many to try, but by stopping as soon as possible we only need to try a tiny fraction of these numbers.
Here we have another advantage of the recursive approach, because this ’early stopping’ is easy to implement. At the moment we fill in our guess for the current position, we can first check if this is a valid guess (e.g. is the digit even). If not, we can ignore it and skip the entire recursive call.
Backtracking sudoku #
For sudoku, the empty cells are basically the unknown digits of our lock. We keep filling empty cells with guesses until we finished the puzzle, or until it becomes unsolvable. In that case we go back to the last cell we guessed (backtracking) and try a different guess.
We have simplified our puzzle to an easier one, although it may not be solvable.
We now recursively use our solver for this easier puzzle. If we find a solution we are done, but of course our guess of ‘1’ could be wrong. In that case the solver will not find a solution. Then we know that ‘1’ was a wrong guess, and we try the next possible digit ‘2’ in the first cell.
Of course we don’t want to fill the entire grid with guesses until we check whether the solution is valid. We want to stop as soon as possible. With the recursive backtracking algorithm this is easy to add: for an empty cell we don’t need to try guesses that are clearly wrong.
For example, in our puzzle there is already a ‘2’ in the first row, so we immediately know that the top left cell cannot be a ‘2’. If a ‘1’ in the top left does not result in a solution, we can skip ‘2’ and immediately move to our next guess ‘3’. But there is also a ‘3’ in the same row (and also in the same column and in the same block), so we skip ‘3’ as well. Our next guess is ‘4’, which does not seem impossible yet. So we fill in the ‘4’ and only now we have to recursively try to solve the remaining puzzle.
Note that in our implementation we will be searching for a solution instead of all solutions. A Sudoku puzzle should have a unique solution, so once we have found one, we assume that this is the only solution. Of course you can extend the program we will be writing to look for more possible solutions.
There is a nice animation of the backtracking algorithm in action on Wikipedia .
As mentioned, the algorithm doesn’t use any clever tricks a human would use, but on the other hand our solver does not really care about the difficulty of the puzzle.
One last thing to note is that our solver will be called recursively, so it can receive a puzzle that is already filled with partial guesses. If we leave the wrong guesses in the puzzle, we cannot keep track of which cells were given and which contain our guesses, so we need to restore the puzzle if we didn’t find a solution.
Fortunately that’s easy: if after trying all possible digits the recursive call didn’t find a solution, we just need to clear the cell that we’ve been guessing before returning.
What we need #
Of course we need to store our puzzle. Our example puzzle is given as a string, but since we need to update our puzzle during solving (by filling in and replacing digits), we want something we can change more easily.
An obvious solution would be a 2-dimensional array, which in Python would be a list of lists, in this case a list of 9 rows, each consisting of a list of 9 digits. A 2-dimensional array works well for rows and columns, but the boxes are a little more complicated.
Another option (and the one we will be using) is to use a single list of 81 numbers, in the same order as given in the input puzzle. Choosing between a 2-dimensional array or a single list is a matter of preference and experience. The single list might seem more complicated for finding rows, columns and boxes, but with a few extra data structures it turns out to be quite easy. I will explain these data structures in detail when we need them, and hopefully you will agree that a single list is a good choice here. But feel free to implement your own version using a 2-dimensional array if you want to try that out.
For reference, here is the layout of the 81-element list:
0 1 2| 3 4 5| 6 7 8
9 10 11|12 13 14|15 16 17
18 19 20|21 22 23|24 25 26
--------+--------+--------
27 28 29|30 31 32|33 34 35
36 37 38|39 40 41|42 43 44
45 46 47|48 49 50|51 52 53
--------+--------+--------
54 55 56|57 58 59|60 61 62
63 64 65|66 67 68|69 70 71
72 73 74|75 76 77|78 79 80
For example, the bottom left cell can be found at index 72.
For the elements of this array we will be using the same characters as in the puzzle input. We could use integers with values 1-9 and use None for an empty cell, but since we don’t need to calculate with these numbers we can just use characters ‘1’-‘9’ and use ‘0’ for an empty cell. This saves some conversion when importing or printing puzzles.
The puzzles from the puzzle bank are given as an 81-character string with ‘0’ representing empty cells, so let’s use that. We can convert this string to a list of 81 characters by just converting the string to a list in Python:
puzzle = `083020090000800100029300008000098700070000060006740000300006980002005000010030540`
grid = list(puzzle)
Implementation #
I started with the sudoku from wikipedia and typed it in as a single string so I had something to start with:
puzzle = (
'53 7 '
'6 195 '
' 98 6 '
'8 6 3'
'4 8 3 1'
'7 2 6'
' 6 28 '
' 419 5'
' 8 79'
)
I used spaces for the empty cells. We could replace them by ‘0’, but
maybe it’s easier to specify the empty cell character as a constant.
Let’s also define some constants for the size. That way, we can use
the same solver for other puzzle sizes. Also, it’s clear what a number
means in the code. SIZE is easier to understand than 9.
We’ll also define a constant with the possible digits, again so we
can use the solver for other sizes (a 16x16 sudoku would need 16
different digits, so we could use characters ‘1’-‘9’ and ‘A’-‘G’
for 10-16).
Let’s start our program by documenting our data structure, and defining
some constants. By only defining SUB_SIZE and calculating the other
numbers, we only have to change a single digit to use the program
for other sizes.
For example, for a 4x4 sudoku we change SUB_SIZE to 2 and set
DIGITS to '1234'.
# Grid numbering:
# We will store the grid in a single list of 81 characters:
# 0 1 2| 3 4 5| 6 7 8
# 9 10 11|12 13 14|15 16 17
# 18 19 20|21 22 23|24 25 26
# --------+--------+--------
# 27 28 29|30 31 32|33 34 35
# 36 37 38|39 40 41|42 43 44
# 45 46 47|48 49 50|51 52 53
# --------+--------+--------
# 54 55 56|57 58 59|60 61 62
# 63 64 65|66 67 68|69 70 71
# 72 73 74|75 76 77|78 79 80
# We will use characters '1'-'9' for digits, '0' for unsolved
# Define the puzzle size (9x9) and the block size (3x3) so
# it's clear where our numbers come from.
SUB_SIZE = 3
SIZE = SUB_SIZE * SUB_SIZE
NUM_CELLS = SIZE * SIZE
DIGITS = '123456789'
EMPTY = '0'
We also add an example puzzle so we can test our code. We use a single 81-character string for the puzzle. For readability, we split the string in rows. Python automatically merges strings on multiple lines, and if we use parenthesis we don’t need line continuation charachters. Note the lack of commas at the end of the lines, otherwise we would have a tuple of 9 strings instead of a single one.
I also added a simple test to make sure we did’t make any mistakes. The assert statement checks if the string is indeed 81 characters, and aborts the program if it’s not.
It would be better to add proper tests, but for this simple implementation we’ll just use asserts. Feel free to convert them to for example doctests.
# example puzzle from the puzzle bank
# (note: no commas, so this is a single string)
diabolical = (
'083020090'
'000800100'
'029300008'
'000098700'
'070000060'
'006740000'
'300006980'
'002005000'
'010030540'
)
# basic check on puzzle input
assert len(diabolical) == NUM_CELLS
In order to check which digits are valid candidates for an empty cell, we need to search for numbers in the same row, column or block. Let’s think about how to do that.
Say we have the cell at offset 42. In our grid numbering, we see that it’s in row 4 (that is the fifth row; the first one is row 0), column 6, and block 5 (blocks are numbered in reading order, so row 1 contains blocks 3, 4, and 5).
We could somehow loop over that row, column, and block, but we would be checking some cells twice. For example cell 44 is in the same row, but also in the same block.
By precomputing some data, we can save time later. The solver may need to check a lot of possibilities, so we want the check to be fast and simple.
For cell 42, we need to check the cells in the corresponding row, column and block once each, so maybe we can precompute the list of cells we need to check. For cell 42, this is cell 36, 37, 38, 39, 40, 41, 43, 44, 6, 15, 24, 33, 51, 60, 69, 78, 34, 35, 52, and 53. Check in the diagram that these are all cells in row 4, in column 6 and in block 5.
We need this for each cell, so let’s try to create a dictionary that maps
each cell to a list of cells we need to check. We’ll call this dict visible,
since it consists of the cells that cell 42 ‘sees’. So visible[42] should
be a list with the 20 numbers given earlier.
Instead of a list, we could actually use a set, since we just need the set of cell offsets. We don’t need a specific order and we want each number only once. Using sets also makes it easier to construct this set, because it is the union of the three sets containing the row, the column and the block.
{1, 2, 3} and {2, 3, 4} will
be the set {1, 2, 3, 4}.
That means, we first need to create sets containing the cell numbers for each row, column, and block.
We also need to know the row, column and block number for a cell, so let’s start with that.
Looking at our grid layout, we have 9 cells per row. That means that we can find the row number by dividing by 9 and rounding down. This is exactly what integer division does. The column number is then the remainder. Another way to see this is to work the other way: if we multiply the row number by 9 and add the column number, we get the cell number.
For 42 (row 4, column 6) we have 42=4*9+6, and 42 // 9 and 42 % 9 result
in 4 and 6.
The blocks are basically a 3x3 grid. We can divide the row and column number
by 3 to get the row and column of this 3x3 grid (row 4 gives 4 // 3 or 1,
which is the second of the three rows 0, 1 and 2). For the block number,
we multiply the block row (0-2) with 3, and add the column number (0-2).
If this sounds complicated, try following the calculations for a few cells.
For example for 42 we already had row 4 and column 6. The 3x3 rows are 4 // 3
and 6 // 3 or row 1, column 2. Recall that we start numbering at 0, so this
is actually the second row and third column of the 3x3 grid of 9 blocks. The
block number is then 3*row + column, or 3*1+2 which is 5.
Now we’re ready to start programming again. Since we usually need all three numbers at the same time (row, column and block number), we’ll put them in a single function, returning a tuple with the three numbers.
# We need some grid geometry to check the rules, so define
# rows, columns and blocks.
def get_position(cell):
"""
For a given cell number, return the row, column, and block number.
"""
row = cell // SIZE
column = cell % SIZE
block = 3 * (row // 3) + (column // 3)
return row, column, block
# simple test
assert get_position(42) == (4, 6, 5)
Now, we need the cell numbers for each row, column and block. We’ll call these groups, since they’re all sets of (9) cell numbers corresponding to a cell. For the solver, it doesn’t really matter if the group is a row, a column or a block.
We shall construct the groups all at once and return them in a dictionary with keys ‘row’, ‘column’ and ‘block’. Each value will be a list of nine sets with the corresponding cell numbers.
For example, group['block'][1] will contain the cell numbers corresponding
to block 1, so {3, 4, 5, 12, 13, 14, 21, 22, 23}.
We will be using a standard programming trick, where we kind of invert the process. Instead of looping over the groups and finding the corresponding cells, we can loop over the cells and find the corresponding groups.
We initialize all groups to an empty set, and then for each cell add that cell number to the correct groups, which we can easily find using the row, column and block number we calculated earlier.
def get_groups():
"""
Create groups for rows, columns and blocks.
Rows are numbered 0-8 top to bottom, columns 0-8 left to right.
Blocks are in reading order:
0 1 2
3 4 5
6 7 8
We create a dictionary that for each type returns a list with 9
elements (e.g. group['rows'] contains the 9 rows). Each element
is a set of cell numbers belonging to that group.
E.g. group['block'][1] = {3, 4, 5, 12, 13, 14, 21, 22, 23}
"""
group = {
'row': [set() for _ in range(SIZE)],
'column': [set() for _ in range(SIZE)],
'block': [set() for _ in range(SIZE)],
}
for cell in range(NUM_CELLS):
row, column, block = get_position(cell)
group['row'][row].add(cell)
group['column'][column].add(cell)
group['block'][block].add(cell)
return group
A simple assert tests if the function works as expected. We don’t need
to keep the test groups, so we throw them away by setting the variable
to None after the assertions.
# Test our groups
test_groups = get_groups()
assert test_groups['row'][4] == {36, 37, 38, 39, 40, 41, 42, 43, 44}
assert test_groups['column'][4] == {4, 13, 22, 31, 40, 49, 58, 67, 76}
assert test_groups['block'][4] == {30, 31, 32, 39, 40, 41, 48, 49, 50}
test_groups = None
Once we have all groups, we can easily find the visible cells for a given cell. We calculate the row, column, and block number, and use it to find the corresponding groups of visible cells. Then, we combine these three groups by taking the union of the three sets. Finally, we can remove the cell itself.
Since we don’t want to do this repeatedly, we store the results in yet another dictionary, that returns for each cell number the set of cells that are visible.
# Now that we have the basic blocks, for each cell create a set of
# cells that are in the same row, column or block. These are exactly
# the cells that need to have a different value than the original
# cell value for a valid sudoku solution.
def get_visible():
"""
Create a dictionary with for each cell number, the numbers of
visible cells (i.e. the cells in its row, column and block)
"""
visible = dict()
groups = get_groups()
for cell in range(NUM_CELLS):
row, column, block = get_position(cell)
row_set = groups['row'][row]
column_set = groups['column'][column]
block_set = groups['block'][block]
visible[cell] = row_set.union(column_set).union(block_set)
visible[cell].remove(cell)
return visible
As a simple test, we use another assert that stores these visible cells in a global variable. Since we need these values in our solver, we don’t throw away the result.
In general it’s better not to use global variables, but we’ll keep this one since it’s a simple program, and we do not want to have to pass these values as parameters to the recursive solver on each call. An alternative is to wrap everything into a class.
# keep global visible so we can use it in backtrack without having
# to pass it as parameter each time
visible = get_visible()
assert visible[42] == {
36, 37, 38, 39, 40, 41, 43, 44, 6, 15, 24, 33,
51, 60, 69, 78, 34, 35, 52, 53
}
With the preliminary work done and the data structures in place, it’s now fairly easy to write the solver. The parameters are the partially filled grid, and a position from where we have to find the first empty cell. We could leave this out and start searching from the top left for the first empty cell, but keeping track of the filled part saves some work here.
We start by printing the current grid values, so you can see the algorithm replacing the 0 values with guesses, and backtracking when it cannot solve the puzzle. This print statement can be removed if you just want to solve the puzzle.
The solver finds the first empty cell, or returns True if there are no more empty cells, in which case the puzzle is solved.
Then, we collect the visible digits, by using our dictionary with visible positions and collecting their content in a set (we only need to collect each digit once). This will also collect 0-values for empty cells, but that’s not a problem because we won’t even try 0 as a guess.
We loop over all possible digits, and see if they’re in the visible set, meaning they’re not valid. If the digit is not in the visible set, it’s a candidate, so we fill it in and call the backtrack function on the remaining puzzle. If that succeeds, we’ve solved the puzzle and we return True to indicate we are done. If not, we try the next digits until we have tried them all.
If we still haven’t found the solution, we restore the cell to empty and return False. In that case the solver will backtrack, replace an earlier guess and try again. That’s why we have to restore the cell, otherwise we would still have a possibly wrong guess left in our puzzle.
def backtrack(grid, position):
"""
Backtracking finds the first unsolved cell and tries each
digit. If the digit is allowed, it recursively tries to solve
the rest of the puzzle.
Since we solve the cells in order, we keep track of our position.
Otherwise we would have to start our search for an unsolved cell
from element 0 each time.
The first time, we can call this function for position == 0.
Return True if solved, and False if not.
"""
# show our progress
print(''.join(grid))
# find an empty cell
while position < NUM_CELLS and grid[position] != EMPTY:
position += 1
# no more empty cells, then we have solved the puzzle
if position == NUM_CELLS:
return True
# collect all digits in visible cells
visible_digits = set()
for cell in visible[position]:
visible_digits.add(grid[cell])
for value in DIGITS:
# only try valid digits
if value not in visible_digits:
# test if value is valid
grid[position] = value
if backtrack(grid, position + 1):
return True
# restore empty cell
grid[position] = EMPTY
return False
Before solving puzzles, let’s add a simple function to show the puzzle as a 9x9 grid. We can join the digits into a single string, and then print 9 slices of substrings.
def print_grid(grid):
puzzle = ''.join(grid)
for line in range(SIZE):
print(puzzle[line*SIZE:(line+1)*SIZE])
In order to solve a puzzle, we call the backtrack function with position 0, to indicate we want to find the first empty cell from the top left.
def solve(grid):
backtrack(grid, 0)
print('Solution:')
print_grid(grid)
Finally, convert our test puzzle string to a list of digits, and see if our solver can find the solution.
grid = list(diabolical)
solve(grid)
If any of the steps is unclear, you can add print statements to see what’s going on. If you’re fairly new to programming and want to make sure you understand everything, a good exercise is to rewrite the solver from scratch without refering to this tutorial.